Romb to czworokąt o wszystkich bokach równej długości, czyli jest równoległobokiem. Inna nazwa rombu to ukośnik. Kwadrat jest szczególnym przykładem rombu o czterech kątach prostych.
W rombie przekątne dzielą się na połowy i przecinają się pod kątem prostym. Natomiast punkt przecięcia przekątnych jest środkiem okręgu wpisanego, którego promień jest połową jego wysokości.
Romb jest figurą wypukłą i suma miar dwóch kątów sąsiednich wynosi 180º. Przekątne rombu dzielą go na cztery przystające trójkąty prostokątne. Opisywana figura geometryczna ma również dwie pary równych kątów i dwie osie symetrii.
Spis treści
Jak obliczyć pole rombu?
Aby obliczyć pole rombu potrzebna jest jego wysokość. Dlatego najpierw wyjaśnimy, czym jest pojęcie wysokości rombu.
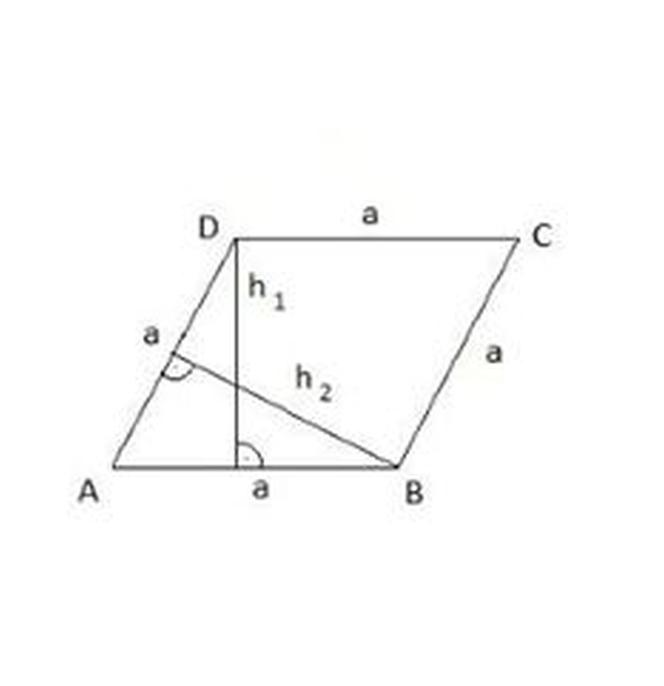
Wysokość rombu oznaczamy literą h. Jest to odległość między przeciwległymi bokami poprowadzona pod kątem prostym.
Ponieważ romb ma wszystkie boki tej samej długości, to odległość między bokami AB i CD jest taka sama jak odległość między bokami AD i BC, a więc h1 = h2.
i
Wzór na pole rombu
Teraz możemy przystąpić do obliczenia rzeczywistego pola rombu.
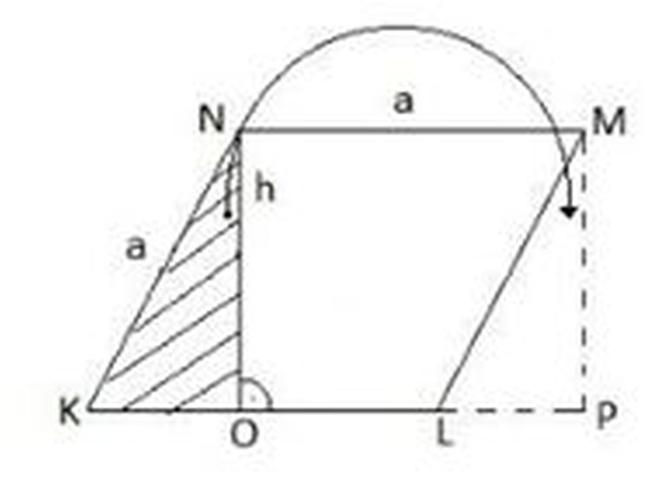
Patrząc na poniższy rysunek wyobraźmy sobie, że mamy romb KLMN, który przecinamy wzdłuż linii ON (wysokość rombu) i w ten sposób otrzymujemy trójkąt KON. Odcięty trójkąt przekładamy tak, jak pokazano na rysunku i otrzymujemy prostokąt OPMN o bokach a i h. Pole rombu KLMN, jest takie samo jak pole prostokąta OPMN.
PKLMN = POPMN
więc pole prostokąta POPMN = /OPI/ · /NO/ gdzie /NO/ = h i /OP/ = a
Tak więc pole rombu wyrażamy wzorem: PKLMN = a · h
Pole rombu jest równe iloczynowi długości boku (a) i wysokości (h) poprowadzonej na ten bok, przy założeniu, że mamy podane długość boku i wysokość.
i
Czytaj również: Pole trójkąta równobocznego - wzór
Pole trapezu - wzór na pole trapezu
Pole powierzchni figury geometrycznej - jak obliczyć?
Jak obliczyć pole rombu?
Teraz rozważymy problem jak obliczyć pole rombu mając podane długości przekątnych (d1 i d2)?
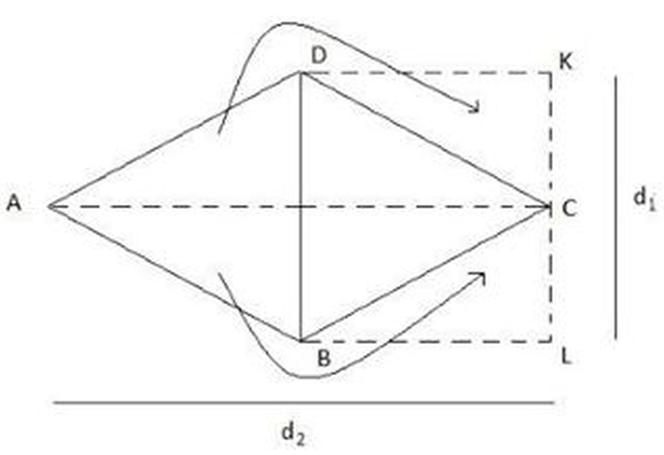
Romb ABCD (rysunek poniżej) przecinamy wzdłuż przekątnych AC i BD.
i
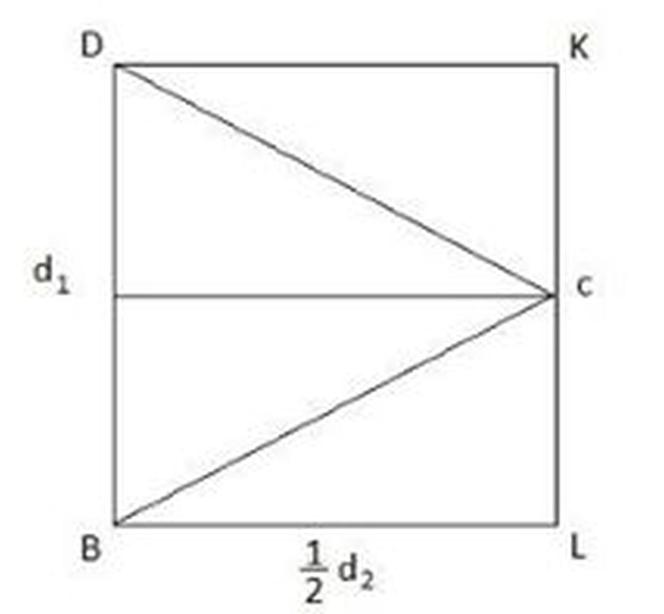
Otrzymujemy cztery trójkąty, które układamy tak, jak na rysunku poniżej.
i
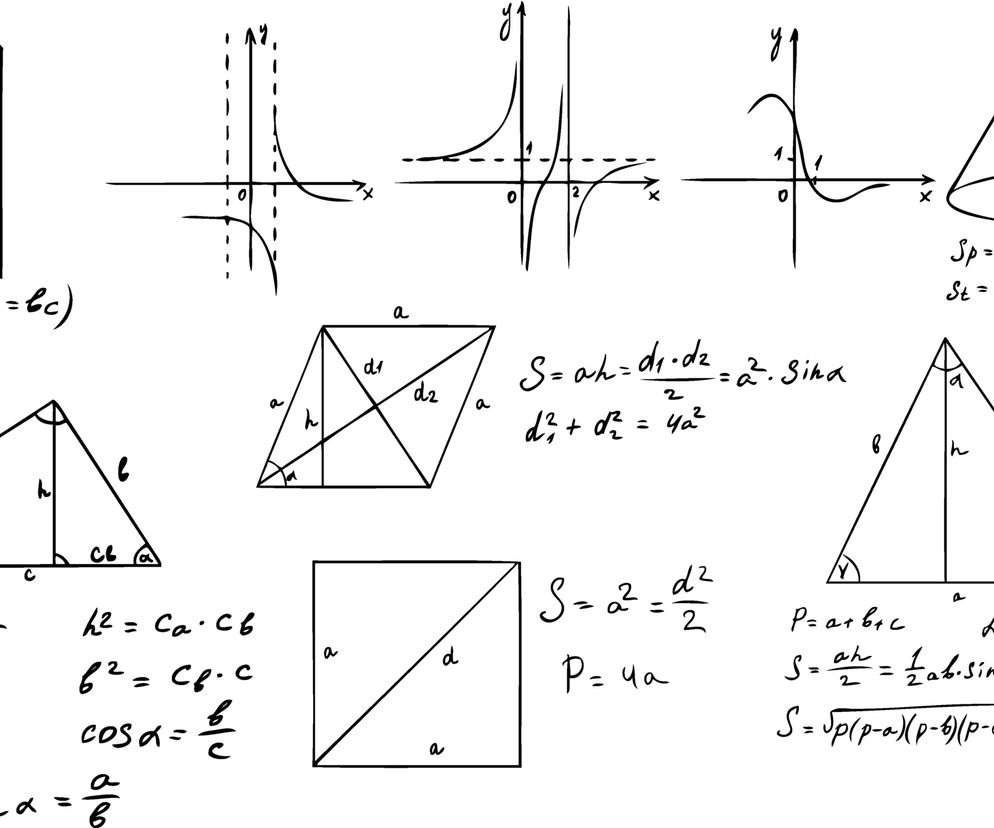
Otrzymujemy prostokąt BLKD. Pole rombu i pole prostokąta są jednakowe: PABCD = PBLKD, a więc pole rombu to 1/2 d1d2Pole rombu = 1/2 ·d1·d2 kiedy mamy podane długości przekątnych.
Zastosowanie poznanych wzorów na przykładzie zadań
Zadanie 1
Przekątne rombu mają długości 6cm i 10cm. Oblicz pole rombu.Mamy podane długości przekątnych rombu, a więc korzystamy ze wzoru PROMBU = 1/2 · d1· d2 = 1/2· 6cm · 10cm = 30cm2
Odp. Pole rombu wynosi 30 cm2
Zadanie 2
Oblicz pole rombu o boku 5cm i wysokości dwa razy krótszej.Obliczamy długość wysokości: h = 5cm : 2 = 2,5cm.Mając podane długości boku i wysokości pole rombu obliczamy korzystając ze wzoru:PROMBU =1/2 · a · h = 1/2 · 5cm · 2,5cm = 12,5cm2
Odp. Pole rombu wynosi 12,5 cm2
Zadanie 3
Pole rombu wynosi 56dm2, a dłuższa przekątna ma długość 140cm. Oblicz długość krótszej przekątnej.Jednostki używane w obliczeniach muszą być jednakowe, więc długość boku wyrazimy w dm: 140cm = 14dm Korzystamy ze wzoru P = 1/2 · d1 · d2 Litery we wzorze zastąpimy liczbami danymi w zadaniu.56 = 1/2 · 14 · d256 = 7 · d2d2 = 56 : 7d2 = 8dm
Odp. Krótsza przekątna rombu wynosi 8 dm
Zadanie 4
Pole rombu jest równe 37cm2, a wysokość poprowadzona na ten bok ma długość 50mm.Oblicz długość boku tego rombu.P = 37cm2h = 50mm = 5cmKorzystamy ze wzoru P = a · hW miejsce liter podstawiamy liczby dane w zadaniu.37 = a · 5a = 37 : 5a = 7,4cm
Odp. Długość boku rombu ma 7,4 cm


![Dyktando klasa 4. Jakie zasady? Pobierz dyktanda dla klasy 4 do wydruku [PDF]](https://cdn.galleries.smcloud.net/t/galleries/gf-cktd-yP6X-DcZN_chlopiec-pisze-przy-biurku-994x828.jpg)
![Dyktando klasa 2. Jakie zasady? Pobierz dyktanda dla klasy 2 do wydruku [PDF]](https://cdn.galleries.smcloud.net/t/galleries/gf-rLv5-E6e3-QzpE_chlopiec-przy-biurku-300x250.jpg)


