Czym są potęgi i potęgowanie?
Potęgi choć wyglądają nietypowo, są niczym innym jak innym zapisem mnożenia. Tabliczkę mnożenia, mnożenie pisemne, a zapewne również mnożenie wszelakich ułamków masz już za sobą, możesz więc być pewny, że potęgi nie powinny ci być straszne. Potęgi służą nam do uproszczenia zapisu długich iloczynów. Dokładniej, tych iloczynów, w których mnożymy przez siebie wiele razy tę samą liczbę. Np. 2 x 2 x 2.
Jak widzisz, pomnożyliśmy przez siebie trzy dwójki. Taki iloczyn mogliśmy przedstawić po prostu jako 2³, gdzie 2 jest nazywane podstawą potęgi, a 3 jest jej wykładnikiem.
Podstawa potęgi mówi nam, jaką liczbę będziemy przez siebie mnożyć. Wykładnik potęgi mówi nam, ile raz to zrobimy.
Jak więc widzisz, podstawowe założenia dotyczące potęg są bardzo proste. Czemu więc sprawiają tyle problemów? A no dlatego, że skoro potęgowanie to nic innego jak mnożenie, to wszystkie operacje, które mogliśmy przeprowadzić na iloczynami, możemy teraz przeprowadzić na potęgach.
O czym pamiętać w czasie potęgowania?
Zanim przejdziemy do podstawowych wzorów i ich wyjaśnień, musisz znać kilka „wyjątkowych” potęg.
Po pierwsze, jeśli potęga ma wykładnik 1, to wynikiem takiego działania jest po prostu liczba, która była podstawą potęgi. Jest to dość intuicyjne, bo skoro: 2² = 2 x 2, to 2¹ = 2
A zatem mamy 4¹ =4, 31¹ =31 itd.
Po drugie, jeśli potęga ma wykładnik 0 to wynikiem takiego działania jest zawsze 1. A zatem 502º = 1, 4º = 1 itd.
Wzory na potęgowanie
Potęgi ułatwiają nam zapisy nie tylko iloczyny tych samych liczb, ale również iloczyny iloczynów, dzielenie przez siebie iloczynów, dodawanie do siebie iloczynów itd. Do tego przydadzą się nam wzory, które niestety będziesz musiał zapamiętać. Postaramy się jednak, żeby były na tyle dobrze wytłumaczone, żeby zapamiętanie ich było czymś więcej niż zakuwaniem.
Po pierwsze, potęgi możemy oczywiście przez siebie mnożyć. Jeśli mają tę samą podstawę to możemy wykorzystać specjalny wzór:
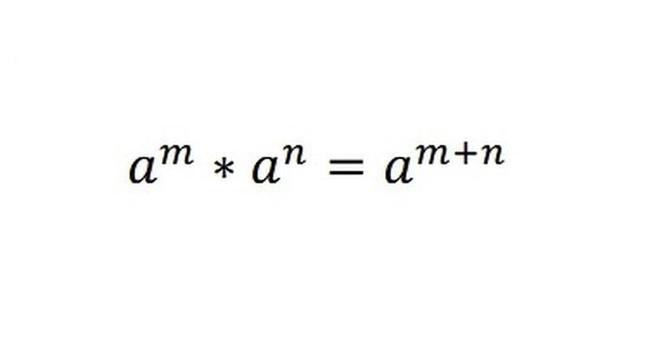
i
Spróbujmy zrozumieć, czemu tak jest. Weźmy prosty przykład, np.:
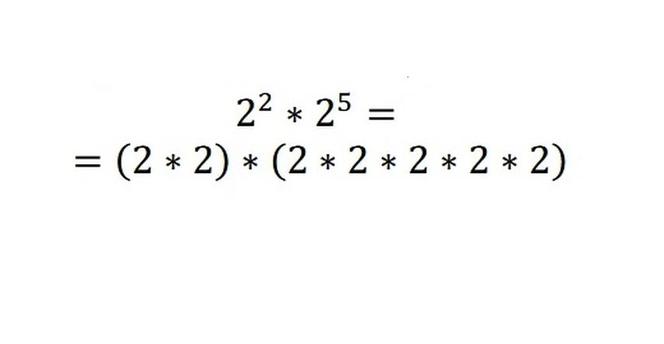
i
Nawiasy nie są tu potrzebne, bo mamy w tym działaniu wyłącznie operacje mnożenia. Jeśli więc opuścimy niepotrzebne nawiasy, zostanie:
2 x 2 x 2 x 2 x 2 x 2 x 2,
a to równanie można zapisać inaczej, tak jak we wzorze:

i
Po drugie, możemy potęgi przez siebie dzielić. Ponownie, jeśli mają tę samą podstawę, z pomocą przychodzi prosty, analogiczny do poprzedniego wzór.
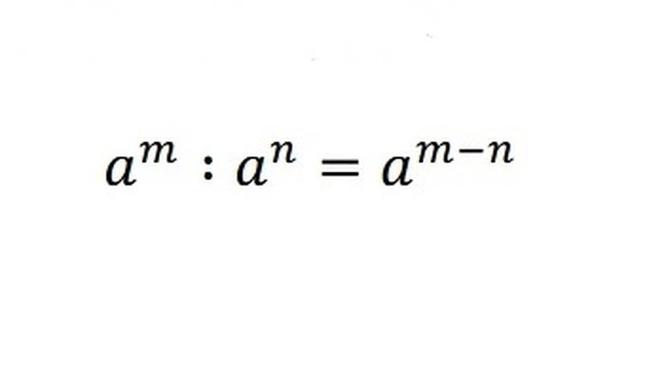
i
Ten przykład łatwiej będzie pokazać zapisując dzielenie w postaci ułamka zwykłego, gdzie kreska ułamkowa posłuży nam jako znak dzielenia.
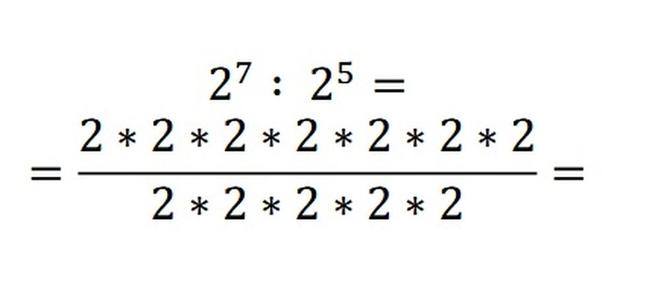
i
Jak pewnie pamiętasz z lekcji o ułamkach zwykłych, w tej sytuacji możemy skrócić mianownik z licznikiem i w tej sytuacji zostanie nam, tak jak we wzorze:
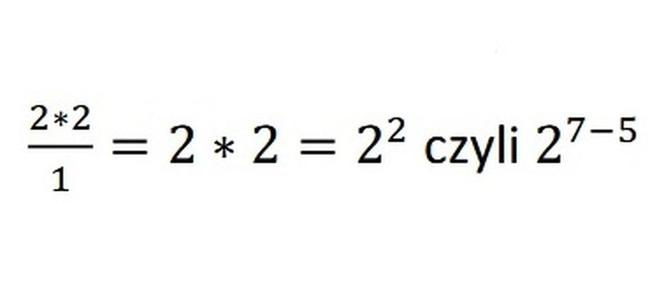
i
Po trzecie potęgi możemy… podnosić do potęgi. Wzór, który nam pomoże, wygląda tak:
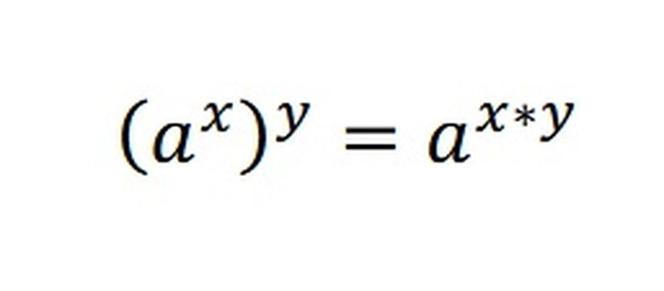
i
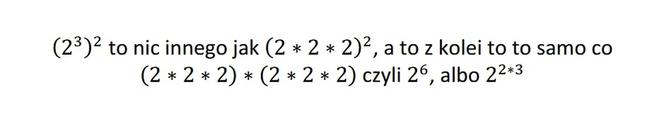
i
Ostatnie wzory, warte poznania to wzory na mnożenie i dzielenie potęg o różnych podstawach, ale tych samych wykładnikach.
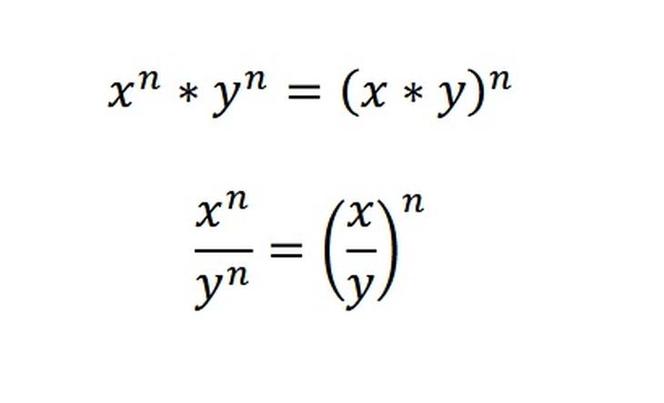
i
Oznacza to na przykład, że 2³ x 4³ to po prostu (2 x 4)³, czyli 8³. Żeby zrozumieć czemu tak jest, spróbujmy rozpisać ten przykład.
2³ x 4³ = 2 x 2 x 2 x 4 x 4 x 4
Mnożenie jest przemienne, więc możemy ustawić czynniki tego iloczynu w dowolnej kolejności. Na przykład tak:
2 x 4 x 2 x 4 x 2 x 4.
Łatwo zauważyć, że powtarza nam się tu mnożenie iloczynu 2 x 4. Potraktujmy go jako jeden czynnik większego iloczynu, żeby było to lepiej widoczne, zapiszemy ten czynnik w nawiasach.
(2 x 4) x (2 x 4) x (2 x 4).
Teraz lepiej widać, że to po prostu (2 x 4)³ czyli 8³.
Czytaj również:
Jak nauczyć dziecko tabliczki mnożenia? Szybkie metody nauki tabliczki mnożenia
Ułamki dziesiętne - jak je zamienić na zwykłe?




![Dyktando klasa 4. Jakie zasady? Pobierz dyktanda dla klasy 4 do wydruku [PDF]](https://cdn.galleries.smcloud.net/t/galleries/gf-cktd-yP6X-DcZN_chlopiec-pisze-przy-biurku-994x828.jpg)
![Dyktando klasa 2. Jakie zasady? Pobierz dyktanda dla klasy 2 do wydruku [PDF]](https://cdn.galleries.smcloud.net/t/galleries/gf-rLv5-E6e3-QzpE_chlopiec-przy-biurku-300x250.jpg)


